Computer chips’ clocks have stopped getting faster. To maintain the regular doubling of computer power that we now take for granted, chip makers have been giving chips more “cores,” or processing units. But how to distribute computations across multiple cores is a hard problem, and this five-part series of articles examines the different levels at which MIT researchers are tackling it, from hardware design up to the development of new programming languages.
In the mid-1990s, Matteo Frigo, a graduate student in the research group of computer-science professor Charles Leiserson (whose work was profiled in the previous installment in this series), developed a parallel version of a fast Fourier transform (FFT). One of the most frequently used classes of algorithms in computer science, FFTs are useful for signal processing, image processing, and data compression, among other things. Steven Johnson, then a graduate student in physics, was using Fourier transforms to solve differential equations and needed FFT software that would run on multiple machines, including parallel machines. “Matteo says, ‘Steven, I have the code for you,’” says Johnson, now an associate professor of applied mathematics. “This is fast and parallel and so forth. I didn’t take his word for it. I took it and I downloaded a half a dozen other FFT programs on the Web, and I benchmarked them on three or four machines, and I made a graph, and I put it up on my Web page. His code was pretty fast, but sometimes faster, sometimes slower than the other codes. His wife said he came home that day and said, ‘Steven put up a Web page that said my code wasn’t the fastest. This has to change.’”
Together, Johnson and Frigo went on to develop software called the fastest Fourier transform in the West, or FFTW, which is, indeed, among the fastest implementations of FFT algorithms for general-purpose computers.
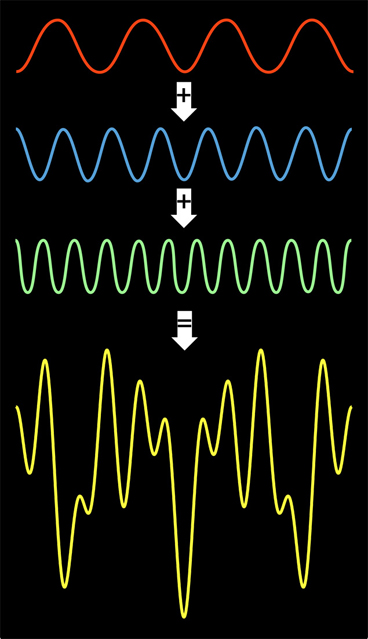
MIT researchers developed one of the fastest software implementations of the Fourier transform, a technique for splitting a signal into its constituent frequencies.
Graphic: Christine Daniloff
Most FFTs use the divide-and-conquer approach described in the last article in this series: data — an incoming audio or video signal, or an image, or a mathematical description of a physical system — is split into smaller parts, whose Fourier transforms are calculated; but those calculations in turn rely on splitting the data into smaller chunks and calculating their Fourier transforms, and so on.
A program that performed all the steps of the FFT calculation in their natural order — splitting the problem into smaller and smaller chunks and then assembling the solution from the bottom up — would end up spending much of its time transferring data between different types of memory. Much of the work that went into FFTW involved maximizing the number of steps a single core could perform without having to transfer the results.
The parallel implementation of FFTW compounds the communication problem, because cores working on separate chunks of the calculation also have to exchange information with each other. If the chunks get too small, communication ends up taking longer than the calculations, and the advantages of parallelization are lost. So every time it’s called upon to run on a new machine, FFTW runs a series of tests to determine how many chunks, of what type, to split the data into at each stage of the process, and how big the smallest chunks should be. FFTW also includes software that automatically generates code tailored to chunks of specific size. Such special-purpose code maximizes the efficiency of the computations, but it would be prohibitively time consuming to write by hand.
According to Jonathan Ragan-Kelley, a graduate student in the Computer Graphics Group at the Computer Science and Artificial Intelligence Laboratory, “Real-time graphics has been probably the most successful mass-market use of parallel processors.” Because updates to different regions of a two-million-pixel image can be calculated largely independently of each other, graphics naturally lends itself to parallel processing. “Your 3-D world is described by a whole bunch of triangles that are made up of vertices, and you need to run some math over all those vertices to figure out where they go on screen,” Ragan-Kelley says. “Then based on where they go on screen, you figure out what pixels they cover, and for each of those covered pixels, you have to run some other program that computes the color of that pixel.” Moreover, he says, computing the color of a pixel also requires looking up the texture of the surface that the pixel represents, and then calculating how that texture would reflect light, given the shadows cast by other objects in the scene. “So you have lots of parallelism, over the vertices and over the pixels,” Ragan-Kelley says.
If a parallel machine were to complete each of the stages in the graphics pipeline — the myriad computations that constitute triangle manipulation, pixel mapping, and color calculation — before the next stage began, it would run into the same type of problem that FFT algorithms can: it would spend much of its time just moving data around. Some commercial graphics software — say, the software that generates images on the Microsoft Xbox — is designed to avoid this problem when it encounters calculations that arise frequently — say, those typical of Xbox games. Like FFTW, the software executes as many successive steps as it can on a single core before transferring data. But outside the narrow range of problems that the software is tailored to, Ragan-Kelley says, “you basically have to give up this optimization.” Ragan-Kelley is investigating whether software could be designed to apply the same type of efficiency-enhancing tricks to problems of graphical rendering generally, rather than just those whose structure is known in advance.
At the International Solid State Circuits conference in San Francisco in February 2011, professor of electrical engineering Anantha Chandrakasan and Vivienne Sze, who received her PhD from MIT the previous spring, presented a new, parallel version of an algorithm common to most computer video systems. Rather than storing every pixel of every frame of video separately, video algorithms store information that can be used to predict the color values of pixels. For instance, one block of pixels might be described as simply having the same color value as the block to its left, or the one above it; another block of pixels might be described as moving six pixels to the right and five down from one frame to the next. Information about pixels ends up taking up less memory than the values of the pixels themselves, which makes it easier to stream video over the Internet.
Different ways of predicting pixel values are described by what are called syntax elements. To save even more space in memory, most video software subjects syntax elements to a further round of data compression. Syntax elements that occur frequently are encoded using very short sequences of bits; syntax elements that occur infrequently are encoded using long sequences of bits.
During playback, however, software has to convert these strings of bits into the corresponding syntax elements. Although today’s high-definition TVs are able to do that conversion on the fly, the TVs of tomorrow, with more than 10 times as many pixels, won’t. Sze and Chandrakasan devised a way to assign the decoding of different types of syntax elements to different cores. Their proposal is currently under review with the MPEG and ITU-T standards bodies, and it could very well end up being incorporated into future video standards.






